Question

Let a, n, b, r, and k be integers. If a = nb+r and k|a and k|b, then k|r

Answer 1

Proof for
`k|r`

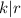
Explanation:

We are given that a, n, b, r and k are integers.

Also,

`a = nb + r`

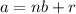
Since k divides a and b, we can write,

a = rk and b = sk, where r and s are integers.

Now, we have to prove that k divides r as well that is
`k|r`

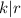
Putting value of a and b in the equation, we get:

`rk = n(sk) + r\\r = rk - nsk\\r = (r-sn)k`

Since, (r-sn) is an integer, k divides r.