Question

For the given function, (a) find the slope of the tangent line to the graph at the given point (b) find the equation of the tangent line. g(x)=2x at x = 9 (a) The slope of the tangent line at x = 9 is

Answer 1

a) The slope of the tangent line to the graph of the function
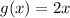`g(x)=2x` at
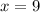`x=9` is 2.

b) The tangent line is
`y=2x`.

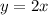Explanation:

a) Tho find the slope of the tangent line to the graph of a given function
`f(x)` at a point
`x_0` we only need to calculate the derivative of
`f(x)` at
`x_0`, i.e.,
`f'(x_0)`.

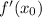For the given function
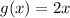`g(x)=2x`, its derivative is
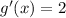`g'(x)=2`. So, in particular, for
`x=9`:
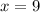`g'(9)=2`. Thus, the slope of the tangent is 2.

b) The equation of the tangent line of the graph of a function
`f(x)` at a point
`x_0` is given by the formula

`y-f(x_0) = f'(x_0)(x-x_0)`.

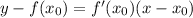In this exercise we have the function
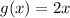`g(x)=2x` and
`x_0=9`. Then,

`g(x_0) = 2x_0 = 2\cdot 9=18`

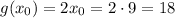
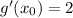`g'(x_0) = 2` (from the previous answer)

So, the equation of the tangent line is

`y-18 = 2(x-9)`

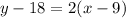
which is equivalent to

`y-18 = 2x-18`

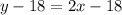
that yields

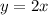`y=2x`.