Answer:
A and C
Explanation:
We are given that two functions are inverses of each other.
We have to find two statements are true about given functions.
Suppose f(x) and g(x) are two functions which are inverses to each other.
When f(x) and g(x) are inverses to each other then
A.
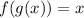 and
and
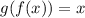
Suppose f(x) =x+2 and g(x)=x-2
f(x) and g(x) are inverses to each other
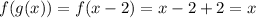
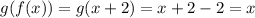
Hence, option A is true.

Suppose ,
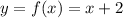
Replace x by y and y replace by x
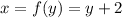
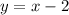
Replace y with

Then, we get
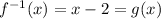
Therefore, the graph of an inverse of a function is a reflection of the function across the lines y=x
Answer:A and C