Question

Use the Bisection Method to find √ 2 correct to roughly within 10^−2 . (Hint: Consider f(x) = x^2 − 2 on [1, 2])

Answer 1

Using the Bisection Method
`√(2) \approx 1.4106`

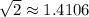
Explanation:

These are the steps for the Bisection Method:

Suppose we need a root for f(x) = 0 and we have an error tolerance of ε

1. Find two numbers a and b at which the function has different signs
2. Define
   `c=(a+b)/(2)`
3. if
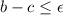   `b-c\leq \epsilon` then accept c as the root and stop
4. if
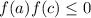   `f(a)f(c)\leq 0` then set c as the new b. Otherwise, set c as the new a. return to step 1.

We know from the information given that

• The function is
  `x^2-2=0`
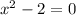
• ε = 0.01

Applying the steps of the Bisection Method you get:

1. There is a root between [1,2] because:

`f(1)=1^2-2=-1\\f(2)=2^2-2=2`

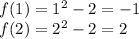
2. Define
`c=(1+2)/(2)=1.5`

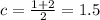
3.
`2-1.5\geq 0.01`

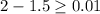
4. Because
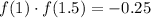`f(1)\cdot f(1.5) = -0.25` we set 1.5 as the new b.

The bisection algorithm is detailed in the following table.

Note that after 7 steps we have
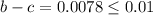`b-c=0.0078 \leq 0.01` hence the required root approximation is c = 1.4106