Answer:
We can prove this theorem as follows:
Explanation:
Let
 where
where
 is a countable set. So we can arrange the elements of
is a countable set. So we can arrange the elements of
 as a sequence
as a sequence
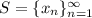 we have the following cases:
we have the following cases:
1. A is finite. If A is finite clearly it is a countable set.
2. A is infinite. Define the sequence of positive integers
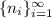 as follows:
as follows:
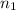 is the less positive integer such that
is the less positive integer such that

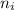 is the less positive integer grater than
is the less positive integer grater than
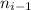 such that
such that
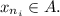 .
.
Now, observe that the correspondence
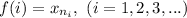 is a one-to-one correspondence between the elements of
is a one-to-one correspondence between the elements of
 and
and
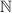 . So,
. So,
 is a countable set.
is a countable set.