Answer:
(a)
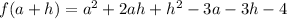
(b)
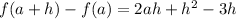
(c)
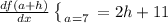
Explanation:
(a)
Simply evaluate (a+h) in the function:
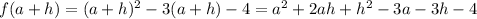
(b)
Evaluate (a) in the function:
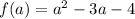
Using the previous answers lets calculate f(a+h)-f(a)
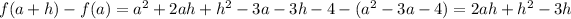
(c) To find the rate of change of f(a+1) when a=7 we need to calculate its derivate at that point:
