Question

Rick has taken a loan of $3,200 from the bank to buy new appliances. His first loan payment is due at the end of this month. He has 24 months to pay off his loan, starting this month. The loan will be compounded monthly at a fixed annual rate of 4.8%.

Use the formula for the sum of a finite geometric sequence to determine Rick's approximate monthly payment.


Rick's approximate monthly payment will be $293.48.

Rick's approximate monthly payment will be $81.27.

Rick's approximate monthly payment will be $128.

Rick's approximate monthly payment will be $140.87.

Answer 1

140

Step-by-step explanation:

Answer 2

Monthly payment of Rick will be approximately $ 140.87

Explantion:

GIVEN :

Loan amount
`P=\$ 3,200`

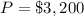
Time duration for loan repayment
`n=24 \mathrm{months}`

Rate of interest
`k=4.8 \% \text { per anuum }`

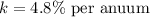
To find:

Rick's monthly payment will be approximately $140.87

Solution:

Using sum of a finite geometric sequence:

`a=P\left[([1-r])/(\left[r-r^(n+1)\right])\right]`

where
`r=(1)/(1+i)`

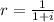
i= monthly interest

but we rate of interest per annum K = 4.8%

now , rate of interest per month,
`i=(4.8)/(12)=0.4 \%=(0.4)/(100)=0.004`

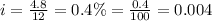
lets find the value of r

`r=(1)/(1+i)`

`r=(1)/(1.004)`

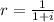
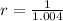
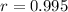`r=0.995` substituting the values,

`a=P\left[(1-r)/(r-r^(n+1))\right]`

`a=3200\left[(1-0.995)/(0.995-0.995^(25))\right]`

`a=3200\left[(0.005)/(0.995-0.882)\right]`

`a=3200\left[(0.005)/(0.118)\right]`

`a=3200[0.044]`

`a=140.8`

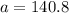
Result :

Hence the approximate monthly payment of Rick is
`$140.87`