Question

Use a proof by cases to show that every perfect square is either a multiple of four or one more than a multiple of four. Hint you only need two cases! 2. Use a proof by cases to show that if two integers are both odd or both even, then their sum is always even 3. Use a proof by contraposition to show that if the sum of two numbers is odd then exactly one of the two numbers must be odd.

Answer 1

Recall that every integer can be written as
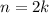`n=2k` or
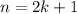`n=2k+1`, i.e., every integer must be even or odd. Let us analyze the first case:

• First case: Assume that the integer
  `n` is even, so
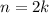  `n=2k` for some integer
  `k`. Then, squaring the equality we have
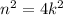  `n^2=4k^2`. Therefore, if
  `n` is even, its square is a multiple of 4.
• Second case: Assume that the integer
  `n` is odd, so
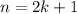  `n=2k+1` for some integer
  `k`. Then, squaring this equality we get
  `n^2=(2k+1)^2=4k^2+4k+1 = 4(k^2+k) +1`. As the number
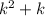  `k^2+k` is an integer, we deduce that
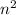  `n^2` is the multiple of 4 plus 1.

As there are no other possibilities, the statement is proven.