Answer:
Recall that a relation is an equivalence relation if and only if is symmetric, reflexive and transitive. In order to simplify the notation we will use A↔B when A is in relation with B.
Reflexive: We need to prove that A↔A. Let us write J for the identity matrix and recall that J is invertible. Notice that
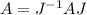 . Thus, A↔A.
. Thus, A↔A.
Symmetric: We need to prove that A↔B implies B↔A. As A↔B there exists an invertible matrix P such that
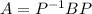 . In this equality we can perform a right multiplication by
. In this equality we can perform a right multiplication by
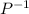 and obtain
and obtain
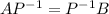 . Then, in the obtained equality we perform a left multiplication by P and get
. Then, in the obtained equality we perform a left multiplication by P and get
 . If we write
. If we write
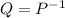 and
and
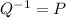 we have
we have
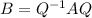 . Thus, B↔A.
. Thus, B↔A.
Transitive: We need to prove that A↔B and B↔C implies A↔C. From the fact A↔B we have
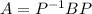 and from B↔C we have
and from B↔C we have
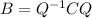 . Now, if we substitute the last equality into the first one we get
. Now, if we substitute the last equality into the first one we get
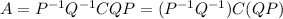 .
.
Recall that if P and Q are invertible, then QP is invertible and
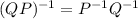 . So, if we denote R=QP we obtained that
. So, if we denote R=QP we obtained that
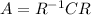 . Hence, A↔C.
. Hence, A↔C.
Therefore, the relation is an equivalence relation.