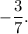Question

Up, Down, and All Around Quiz

Points (-5, 8) and D (2, 5) lie on line CD. If
points C" and D' are created by translating
points C and D left 6 units, what is the slope of line
C'D' ?​

Answer 1

hey

Explanation:

sorrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrry to bother you but do you know the answers i want to check mine please

Answer 2

Answer: The required slope of line C'D' is
`-(3)/(7).`

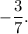
Step-by-step explanation: Given that the points (-5, 8) and D (2, 5) lie on line CD. And, the points C' and D' are created by translating points C and D left 6 units.

We are to find the slope of line C'D'.

We know that

if a point (x, y) is translated 6 units left, then its new co-ordinates becomes

(x, y) ⇒ (x-6, y).

So, after translating 6 units left, the co-ordinates of points C(-5, 8) and D(2, 5) becomes

C(-5, 8) ⇒ C'(-5-6, 8) = (-11, 8),

D(2, 5) ⇒ D'(2-6, 5) = (-4, 5).

We know that the slope of a line having points (a, b) and (c, d) on it is given by

`m=(d-b)/(c-a).`

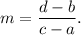
Therefore, the slope of line C'D' is

`m=(5-8)/(-4-(-11))=(-3)/(-4+11)=-(3)/(7).`

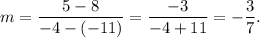
Thus, the required slope of line C'D' is
`-(3)/(7).`