Answer:
magnitude = 304.14 km/h
direction:
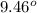 West of North
West of North
Step-by-step explanation:
The final plane's vector velocity will be the result of the vector addition of one pointing North of length 300 km/h, another one pointing West of length 50 km/h.
To find the magnitude of the final velocity vector (speed) we need to apply the Pythagorean theorem in a right angle triangle with sides: 300 and 50, and find its hypotenuse:
 km/h
km/h
The actual direction of the plane is calculated using trigonometry, in particular with the arctan function, since the tangent of the angle can be written as:
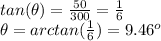
So the resultant velocity vector of the plane has magnitude = 304.14 km/h,
and it points
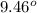 West of the North direction.
West of the North direction.