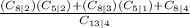Question

There is a group of 5 seniors and 8 first year graduate students to fill the openings of local news reporters. Suppose that we pick 4 students, who are randomly picked from this pool for interviews. Using this given information, calculate the following:

1.) Find the probability that at least 2 first year graduate students are among the chosen group. Please note that this is a combinatorics problem and the answer can be left in terms of C k,n. Please show all work.

Answer 1

`((C_(8|2)) (C_(5|2) ) + (C_(8|3) )(C_(5|1) )+ C_(8|4))/(C_(13|4) )`

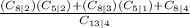
Explanation:

The total amount of students in the pool is 13.

1) Find the probability that at least 2 first year graduate students are among the chosen group.

The total amount of different ways to chose 4 students from a pool of 13 is
`C_(13|4)`

The total amount of ways to choose at least 2 first year graduate students would be:

Ways of choose 2 first year students and 2 seniors + ways of choose 3 first year students and 1 senior + ways of choose 4 first year students. (we are adding and not multiplying because it's "choose 2 first year OR 3 OR 4")

Therefore, the probability would be:

`((C_(8|2)) (C_(5|2) ) + (C_(8|3) )(C_(5|1) )+ C_(8|4))/(C_(13|4) )`