Answer : The entropy change of reaction for 1.62 moles of
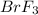 reacts at standard condition is 217.68 J/K
reacts at standard condition is 217.68 J/K
Explanation :
The given balanced reaction is,
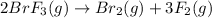
The expression used for entropy change of reaction
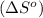 is:
is:
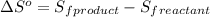
![\Delta S^o=[n_(Br_2)* \Delta S_f^0_((Br_2))+n_(F_2)* \Delta S_f^0_((F_2))]-[n_(BrF_3)* \Delta S_f^0_((BrF_3))]](https://img.qammunity.org/2020/formulas/chemistry/college/62h4f2ajev212va5ubt91iu1q2sea0ph7x.png)
where,
 = entropy change of reaction = ?
= entropy change of reaction = ?
n = number of moles
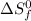 = standard entropy of formation
= standard entropy of formation
 = 245.463 J/mol.K
= 245.463 J/mol.K
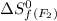 = 202.78 J/mol.K
= 202.78 J/mol.K
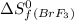 = 292.53 J/mol.K
= 292.53 J/mol.K
Now put all the given values in this expression, we get:
![\Delta S^o=[1mole* (245.463J/K.mole)+3mole* (202.78J/K.mole)}]-[2mole* (292.53J/K.mole)]](https://img.qammunity.org/2020/formulas/chemistry/college/r0xnk69schw3xgwh769w5n4xj33jxtbw6s.png)
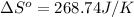
Now we have to calculate the entropy change of reaction for 1.62 moles of
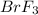 reacts at standard condition.
reacts at standard condition.
From the reaction we conclude that,
As, 2 moles of
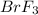 has entropy change = 268.74 J/K
has entropy change = 268.74 J/K
So, 1.62 moles of
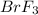 has entropy change =
has entropy change =
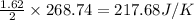
Therefore, the entropy change of reaction for 1.62 moles of
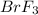 reacts at standard condition is 217.68 J/K
reacts at standard condition is 217.68 J/K