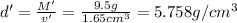Question

A pycnometer is a precisely weighted vessel that is used for highly accurate density determinations. Suppose that a pycnometer has a mass of 27.60 g when it is empty and has a mass of 45.65 g when it is completely filled with water at 20 °C. A 9.5 g metal ingot is placed in the pycnometer. When it is then filled with water at 20 °C, the total mass is 56.83 g. If the density of water at 20 °C is 998.2 kg/m3, what is the density of the metal ingot in grams per cubic centimeter.

Answer 1

5.758 is the density of the metal ingot in grams per cubic centimeter.

Step-by-step explanation:

1) Mass of pycnometer = M = 27.60 g

Mass of pycnometer with water ,m= 45.65 g

Density of water at 20 °C = d =
`998.2 kg/m^3`

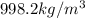
1 kg = 1000 g

`1 m^3=10^6 cm^3`

`998.2 kg/m^3=(998.2 * 1000 g)/(10^6 cm^3)=0.9982 g/cm^3`

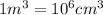
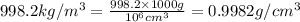
Mass of water ,m'= m - M = 45.65 g - 27.60 g =18.05 g

Volume of pycnometer = Volume of water present in it = V

`Density=(Mass)/(Volume)`

`V=(m')/(d)=(18.05 g)/(0.9982 g/cm^3)=18.08 cm^3`

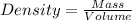
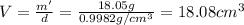
2) Mass of metal , water and pycnometer = 56.83 g

Mass of metal,M' = 9.5 g

Mass of water when metal and water are together ,m''= 56.83 g - M'- M

56.83 g - 9.5 g - 27.60 g = 19.7 g

Volume of water when metal and water are together = v

`v=(m'')/(d)=(19.7 g)/(0.9982 g/cm^3)=19.73 cm^3`

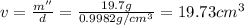
Density of metal = d'

Volume of metal = v' =
`(M')/(d')`

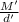
Difference in volume will give volume of metal ingot.

v' = v - V

`v'=19.73 cm^3-18.08 cm^3=`

`v'=1.65 cm^3`

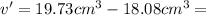
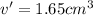
Since volume cannot be in negative .

Density of the metal =d'

=
`d'=(M')/(v')=(9.5 g)/(1.65 cm^3)=5.758 g/cm^3`