Answer:
The vapor pressure at temperature 363 K is 0.6970 atm
The vapor pressure at 383 K is 1.410 atm
Step-by-step explanation:
To calculate
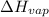 of the reaction, we use clausius claypron equation, which is:
of the reaction, we use clausius claypron equation, which is:
![\ln((P_2)/(P_1))=(\Delta H_(vap))/(R)[(1)/(T_1)-(1)/(T_2)]](https://img.qammunity.org/2020/formulas/chemistry/college/4vtbgz8qequ3vvsclhkmmvxlsikmj2gcnu.png)
where,
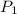 = vapor pressure at temperature
= vapor pressure at temperature
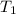
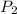 = vapor pressure at temperature
= vapor pressure at temperature
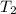
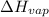 = Enthalpy of vaporization
= Enthalpy of vaporization
R = Gas constant = 8.314 J/mol K
1)
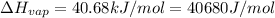
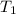 = initial temperature =363 K
= initial temperature =363 K
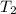 = final temperature =373 K
= final temperature =373 K
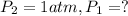
Putting values in above equation, we get:
![\ln((1 atm)/(P_1))=(40680 J/mol)/(8.314J/mol.K)[(1)/(363)-(1)/(373)]](https://img.qammunity.org/2020/formulas/chemistry/college/idbotplrpf0jy53npvn3yvzrfapcbm9em0.png)
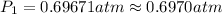
The vapor pressure at temperature 363 K is 0.6970 atm
2)
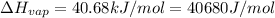
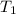 = initial temperature =373 K
= initial temperature =373 K
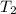 = final temperature =383 K
= final temperature =383 K
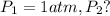
Putting values in above equation, we get:
![\ln((P_2)/(1 atm))=(40680 J/mol)/(8.314J/mol.K)[(1)/(373)-(1)/(383)]](https://img.qammunity.org/2020/formulas/chemistry/college/pvsdv55i2udfu4399o2gps64mxfhdsb339.png)
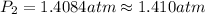
The vapor pressure at 383 K is 1.410 atm