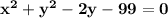Answer:
The equation of the circle with center (0, 1) and a radius of 10 is
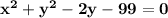
Solution:
Equation of circle whose center (h, k) and radius r is given as,
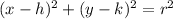 ---- eqn 1
---- eqn 1
From question, given that the circle has radius 10 and center (0, 1). We have to find the equation of the circle.
Hence we get, h = 0 ; k = 1; r = 10
By using eqn 1, the equation of circle whose center (0, 1) and radius 10 is given as
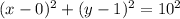
On Simplifying we get
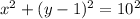
Expand
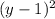 using the formula
using the formula
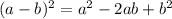
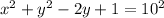
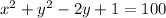
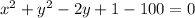
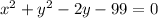
Hence equation of the circle with center (0, 1) and a radius of 10 is