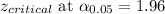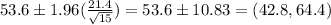Question

Given values: 54, 65, 76, 43, 45, 76, 87 12, 23, 34, 67,65, 78, 45, 34. Given 95% confidence and sigma (population standard deviation) (12) Compute the confidence interval. Round to one decimal place.

(A) (47.5, 59.7)

(B) (12, 87)

(C) (48.5, 58.7)

(D) None of the above.

Answer 1

Option (D) None of the above.

Explanation:

We are given the following data:

54, 65, 76, 43, 45, 76, 87, 12, 23, 34, 67,65, 78, 45, 34

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

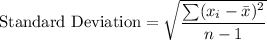
where
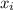`x_i` are data points,
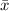`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(804)/(15) = 53.6`

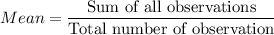
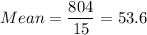
Sum of squares of differences = 0.16 + 129.96 + 501.76 + 112.36 + 73.96 + 501.76 + 1115.56 + 1730.56 + 936.36 + 384.16 + 179.56 + 129.96 + 595.36 + 73.96 + 384.16 = 6849.6

`S.D = \sqrt{(6849.6)/(15)} = 21.4`

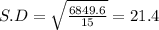
Confidence interval:

`\mu \pm z_(critical)(\sigma)/(√(n))`

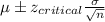
Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

`53.6 \pm 1.96((21.4)/(√(15)) ) = 53.6 \pm 10.83 = (42.8,64.4)`