Question

A standard 1.00 kg mass is to be cut from a bar of steel having an equilateral triangular cross section with sides equal to 2.50 in. The density of the steel is 7.70 g/cm3. How many inches long must the section of bar be?

Answer 1

The section of the bar is 2.92 inches.

Step-by-step explanation:

Mass of the steel cut ,m = 1.00 kg = 1000 g

Volume of the steel bar = V = Area × height

Height of the of the section of bar = h

Area of Equilateral triangular =
`(√(3))/(4)a^2`

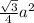
a = 2.50 inches

Cross sectional area of the steel mass = A

`A=(√(3))/(4)(2.50 inches)^2=2.71 inches^2`

`V = 2.71 inches^2* h`

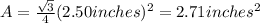
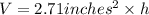
Density of the steel = d =
`7.70 g/cm^3`

`1cm^3 = 0.0610237 inches^3`

`d=(m)/(v)`

`(7.70 g)/(0.0610237 inches^3)=( 1000 g)/(2.71 inches^2* h)`

`h=( 1000 g* 0.0610237 inches^3)/(2.71 inches^2* 7.70 g)`

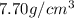
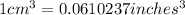
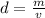
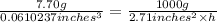
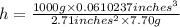
h = 2.92 inches

The section of the bar is 2.92 inches.