Question

Solve the absolute value inequality|2x+3|≥|x−7|

Answer 1

Answer:
`x\geq 7`

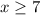
Explanation:

Given

`|2x+3|\geq |x-7|`

here we will divide x interval in 3 case

case
`x<(-3)/(2)`

let us take x=-2

|-1| is not greater than |-9|

thus
`x<(-3)/(2)` is not possible

Case
`(-3)/(2)<x<7`

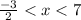
Take x=0

|3| is less than |-7|

thus for
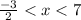`(-3)/(2)<x<7` equality is not satisfied

Case 3
`x\geq 7`

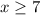
take x=7

|17| is greater than |0|

Thus for
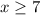`x\geq 7` is the required region