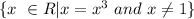Question

Use set-builder notation to describe the following sets: (a) {1,2,3,4,5,6,7} (b) {1, 10, 100, 1000, 10000} (c) {1,1/2, 1/3, 1/4,1/5, ...} (d) {0}

Answer 1

A) The set builder notation is: n∈Z, 1≤n≤7.

B) The set builder notation is:
`\ x=0,1,2,3,4\`

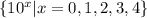
C) The set builder notation is:
`\ n\in z\`

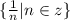
D) The set builder notation can be:
`\ x=x^3\ and\ x\\eq 1\`

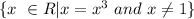
Explanation:

Consider the provided information,

We need to use set-builder notation to describe the following sets.

(a) {1,2,3,4,5,6,7}

Here, the number are integer starting from 1 to 7.

Thus, the set builder notation is: n∈Z, 1≤n≤7.

(b) {1, 10, 100, 1000, 10000}

The above set can be written as:

`\{1, 10, 100, 1000, 10000\}=\{10^0, 10^1, 10^2, 10^3, 10^4\}`

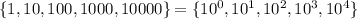
Thus, the set builder notation is:
`\ x=0,1,2,3,4\`

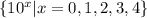
(c) {1, 1/2, 1/3, 1/4, 1/5, ...}

Here the numerator is 1 for each term but denominator is natural number.

Thus, the set builder notation is:
`\(1)/(n)`

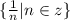
(d) {0}

The set builder notation can be:
`\ x=x^3\ and\ x\\eq 1\`