Question

Given the following Demand Curve: P = 24 - 8Q

Express this Demand Curve in terms of Q.
Use either the original equation or the one in part (a) and find P if Q=2.
Use either the original equation or the one in part (a) and find Q if P = 8.
Write out the equation for total revenue in terms of Q.
Write out the equation for marginal revenue in terms of Q. Hint: Marginal revenue is the first derivative of total revenu
Find the values of P and Q that will maximize total revenue.
Calculate this maximum value of total revenue.

Answer 1

Maximum value of total revenue = 18

Explanation:

• Express this Demand Curve in terms of Q.

P = 24 - 8Q (it is the same equation)

• Find P, if Q=2

P= 24-8(2)

P=24-16

P=8

• Find Q if P = 8.

P = 24 - 8Q

8= 24 - 8Q

8Q= 24-8

8Q=16

Q=16/8

Q=2

• Total revenue in terms of Q

Total revenue is P times Q, that is

P*Q=TR=(24-8Q)*Q

TR=24Q-8Q^2

`TR=24Q-8Q^(2) \\\\`

• Marginal Revenue

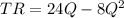
It is the first derivative of TR

TR'(Q)= 24-16Q

• Find the values of P and Q that will maximize total revenue.

To find them first TR'(Q)=0, that is

0=24-16Q

16Q=24

Q=24/16

Q=3/2

Q=1.5

and we plug in 1.5 in P=24-8Q, which is,

P=24-8Q

P=24-8(1,5)

P=24-12

P=12

• Calculate this maximum value of total revenue

P=12 Q=1.5

P*Q=Total Revenue

12*1.5=Total Revenue

18=Total Revenue