Answer:
a) The first term is a=7
b) The common difference is d=3
c) The sum of the first 15 term is 420.
Explanation:
Given : If the fifth term of a AP is 19 and the tenth term is 34.
To find : a) the first term b) The common difference c) The sum of the first 15 term ?
Solution :
The Arithmetic progression is in the form,
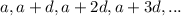
Where, a is the first term and d is the common difference
The nth term of the A.P is
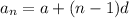
The fifth term of a AP is 19.

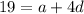 ...(1)
...(1)
The tenth term is 34.
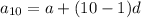
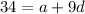 ...(2)
...(2)
Solving (1) and (2) by subtracting the equations,
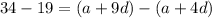
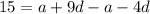
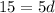
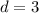
Substitute in (1),
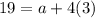
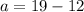
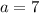
a) The first term is a=7
b) The common difference is d=3
c) The sum of the first 15 term is given by,
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2020/formulas/mathematics/high-school/p82o14tt1akmx6szgemiszk1cohd2h7amw.png)
![S_(15)=(15)/(2)[2(7)+(15-1)3]](https://img.qammunity.org/2020/formulas/mathematics/college/85etz16txywd8cs7jk3h3v1u0td76814so.png)
![S_(15)=(15)/(2)[14+(14)3]](https://img.qammunity.org/2020/formulas/mathematics/college/qrl9xmah76rwt1cdp0sr11ltwdxs17d2dk.png)
![S_(15)=(15)/(2)[14+42]](https://img.qammunity.org/2020/formulas/mathematics/college/o6h4tpsiv6j07g3ob4kipt6ghb2ucpofv9.png)
![S_(15)=(15)/(2)[56]](https://img.qammunity.org/2020/formulas/mathematics/college/22elblcfopv5avzz4xl97c3jpgd82vrore.png)
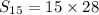
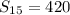
The sum of the first 15 term is 420.