Question

Find the particular solution of the differential equation dy + 7y = 6 satisfying the initial condition y(0) = 0. Answer: y= Your answer should be a function of x.

Answer 1

Explanation:

We have the equation
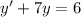`y'+7y=6` with the initial condition
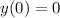`y(0)=0`. It is not difficult to notice that this is a linear equation, which has the general expression

`y'+P(x)y=Q(x)`.

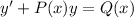The solution of this equation is expressed by a general formula:

`y(x) = \exp\left(-\int P(x)dx\right)\left(\int Q(x)\exp\left(-\int P(x)dx\right) +C\right)`.

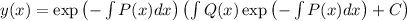In the particular case of our equation, we have

`P(x)=7`

`Q(x)=6`.

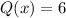Then, we must calculate the integrals

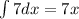`\int 7dx = 7x` that implies

`\exp\left(-\int P(x)dx\right) = e^(-7x)`,

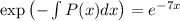and

`\int 6e^(7x)dx = (6)/(7)e^(7x)`

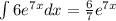
Then,

`y(x) = e^(-7x)\left((6)/(7)e^(7x) +C\right) = (6)/(7) + Ce^(-7x)`.

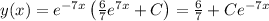In order to obtain the value of the constant we substitute the initial condition

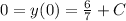`0=y(0) = (6)/(7) + C` that implies
`C=-(6)/(7)`

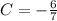
Therefore,

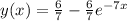`y(x) = (6)/(7)-(6)/(7)e^(-7x)`.