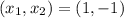Question

Convert the system 3x1 5x2 -2 = 6x1 7x2 -1 to an augmented matrix. Then reduce the system to echelon form and determine if the system is consistent. If the system in consistent, then find all solutions. Augmented matrix: Echelon form: Is the system consistent? select ( Solution: (x1, x2) = + + S1 Help: To enter a matrix use [[ 1. For example, to enter the 2 x 3 matrix 2 you would type [[1,2,3),(6,5,4]1, so each inside set of [) represents a row. If there is no free variable in the solution, then type 0 in each of the answer blanks directly before each s. For example, if the answer is (x,x2)= (5,-2), then you would enter (5 +0s1,-2 + 0s1). If the system is inconsistent, you do not have to type anything in the "Solution" answer blanks. I

Answer 1

`3x_1+5x_2=-2\\6x_1+7x_2=-1`

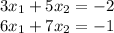
The augmented matrix associated to the linear system is

`\left[\begin{array}{ccc}3&5&-2\\6&7&-1\end{array}\right]`

Using row operations we reduce the system to echelon form:

1. We substract to the second row three times the first row and obtain the matrix

`\left[\begin{array}{ccc}3&5&-2\\0&-3&3\end{array}\right]` that is the echelon form of the system.

Now we use backward substitution to find the solution.

1.
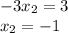
`-3x_2=3\\x_2=-1`

2.
`3x_1+5x_2=-2\\3x_1+5(-1)=-2\\x_1=1`

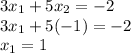
The the unique solution is
`(x_1,x_2)=(1,-1)`