Question

What is the speed of a 3 cm diameter roll if it has a velocity of 1220 yards/hour?

Answer 1

The speed of the roll is 1239.52 revolutions per minut (1239.52 rpm).

Explanation:

In this problem we want to know the angular speed of the roll, knowing its tangencial speed (1220 yards/hour).

The relation between the angular speed and the tangencial speed is

`v=\omega*r=\omega*(D/2)`

`\omega=2v/D`

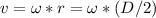
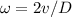
In this case we have a diameter of 3 cm and a velocity of 1220 yards/hour. So we can write

`\omega=2v/D=2*1220(yards)/(hour) *(1)/(3\,cm) *(91.44cm)/(1 yard) *(1hour)/(60min)= 1239.52 (1)/(min)=1239.52 rpm`

So the speed of the roll is 1239.52 revolutions per minut (1239.52 rpm).