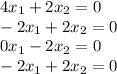Question

Convert the augmented matrix 4 2 -2 2 0 -2 -2 2 to the equivalent linear system. Use x1 and x2 to enter the variables x1 and x2. Note: You can earn partial credit on this problem. Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining.

Answer 1

We have the following system

`\left[\begin{array}{cc}4&2\\-2&2\\0&-2\\-2&2\end{array}\right] \left[\begin{array}{cc}x_1\\x_2\end{array}\right]=\left[\begin{array}{ccc}0\\0\\0\\0\end{array}\right]`

The column 1 represent the coeficients of the unknown
`x_1`, and the column 2 represent the values of the coefficients of the unknown
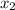`x_2`. Then the k-th component of each column represents the coefficient of the unknowns in the k-th equation of the linear system.

So the corresponding linear system is

`4x_1+2x_2=0\\-2x_1+2x_2=0\\0x_1-2x_2=0\\-2x_1+2x_2=0`