Question

Numerically estimate the slope of y = f(x) at r = a. 1. f(x) = x^2 - 2x, a = 2 2. f(x) = sin 2x, a = 0

Answer 1

1. Slope at a=2 is 2.

2. Slope at a=0 is 2.

Explanation:

We need to find the slope of y = f(x) at x = a.

1.

The given function is

`f(x)=x^2-2x`

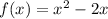
It can be written as

`y=x^2-2x`

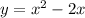
Differentiate with respect to x.

`y'=2x-2`

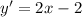
Substitute x=2 to find the slope of y = f(x) at a=2.

`y'=2(2)-2`

`y'=4-2`

`y'=2`

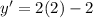
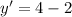
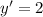
Therefore the slope of function at a=2 is 2.

2.

The given function is

`f(x)=\sin 2x`

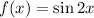
It can be written as

`y=\sin 2x`

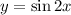
Differentiate with respect to x.

`y'=2\cos 2x`

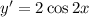
Substitute x=0 to find the slope of y = f(x) at a=0.

`y'=2\cos 2(0)`

`y'=2(1)`

`y'=2`

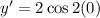
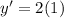
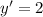
Therefore the slope of function at a=0 is 2.