Answer:
The complex number
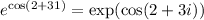 has Cartesian form
has Cartesian form
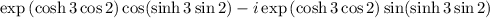 .
.
Explanation:
First, we need to recall the definition of
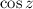 when
when
 is a complex number:
is a complex number:
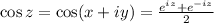 .
.
Then,
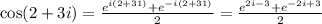 . (I)
. (I)
Now, recall the definition of the complex exponential:
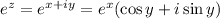 .
.
So,
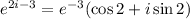
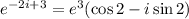 (we use that
(we use that
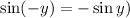 .
.
Thus,
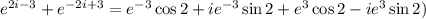
Now we group conveniently in the above expression:
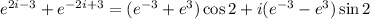 .
.
Now, substituting this equality in (I) we get
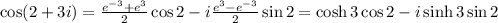 .
.
Thus,
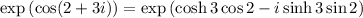
![\exp\left(\cos(2+3i)\right) = \exp\left(\cosh 3\cos 2\right)\left[ \cos(\sinh 3\sin 2)-i\sin(\sinh 3\sin 2)\right]](https://img.qammunity.org/2020/formulas/mathematics/college/g6hfsdh26psvektioe8zjp5wha2xzxl766.png) .
.