Question

What is this function written in vertex form?

The image shows a geometric representation of the
function f(x) = x2 + 2x + 3 written in standard form
f(x) = (x + 2)2 +3
f(x) = (x2 + 2x)2 + 3
f(x) = (x + 1)2 + 2
f(x) = (x + 3)2 + 2%
+X
+
+
+

Answer 1

c

Explanation:

Answer 2

`f(x) = (x+1)^(2) + 2`

Explanation:

In order to change a quadratic equation to vertex form, you can follow these steps:

quadratic form:
`f(x) = x^(2)  +2x +3`

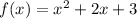
Transfer 3 to the other side of the equation, so add -3 to both sides of the equation and simplify.

`f(x) -3 = x^(2)  +2x +3 - 3`

`f(x) -3 = x^(2)  +2x`

Now if you look at the expression if you add 1 to both sides of the equation you will complete the perfect square trinomial

`f(x) -3 + 1 = x^(2)  +2x + 1`

`f(x) - 2 = x^(2)  +2x + 1`

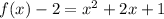
Write the trinomial factors:

`f(x) - 2 = (x + 1)(x  + 1) ---> f(x) + 2 = (x^(2)  + 1)^(2)`

Finally simplify, clear f(x)

`f(x)  = (x^(2)  + 1)^(2) + 2`

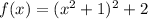
Now it has the form
`f(x) = a(x -h)^(2) + k`

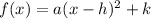
then (h, k) will be = (-1, 2)