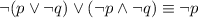Answer:
The statement
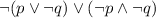 is equivalent to
is equivalent to
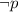 ,
,
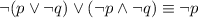
Explanation:
We need to prove that the following statement
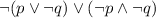 is equivalent to
is equivalent to
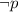 with the use of Theorem 2.1.1.
with the use of Theorem 2.1.1.
So
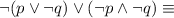
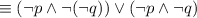 by De Morgan's law.
by De Morgan's law.
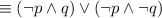 by the Double negative law
by the Double negative law
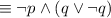 by the Distributive law
by the Distributive law
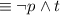 by the Negation law
by the Negation law
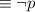 by Universal bound law
by Universal bound law
Therefore