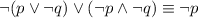Question

Use Theorem 2.1.1 to verify the logical equivalence. Give a reason for each step. -(pv –q) v(-p^q) = ~p

Answer 1

The statement
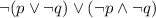`\lnot(p\lor\lnot q)\lor(\lnot p \land \lnot q)` is equivalent to
`\lnot p`,
`\lnot(p\lor\lnot q)\lor(\lnot p \land \lnot q) \equiv \lnot p`

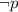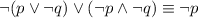
Explanation:

We need to prove that the following statement
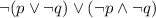`\lnot(p\lor\lnot q)\lor(\lnot p \land \lnot q)` is equivalent to
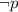`\lnot p` with the use of Theorem 2.1.1.

So

`\lnot(p\lor\lnot q)\lor(\lnot p \land \lnot q) \equiv`

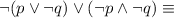
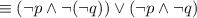`\equiv (\lnot p \land \lnot(\lnot q))\lor(\lnot p \land \lnot q)` by De Morgan's law.

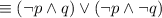`\equiv (\lnot p \land q)\lor(\lnot p \land \lnot q)` by the Double negative law

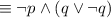`\equiv \lnot p \land (q \lor \lnot q)` by the Distributive law

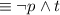`\equiv \lnot p \land t` by the Negation law

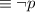`\equiv \lnot p` by Universal bound law

Therefore
`\lnot(p\lor\lnot q)\lor(\lnot p \land \lnot q) \equiv \lnot p`