Answer:
The statement
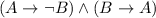 is a contingency.
is a contingency.
The statement
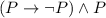 is a contradiction.
is a contradiction.
Explanation:
A tautology is a proposition that is always true.
A contradiction is a proposition that is always false.
A contingency is a proposition that is neither a tautology nor a contradiction.
a) To classify the statement
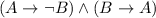 , you need to use the logic laws as follows:
, you need to use the logic laws as follows:
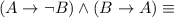
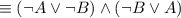 by the logical equivalence involving conditional statement.
by the logical equivalence involving conditional statement.
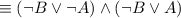 by the Commutative law.
by the Commutative law.
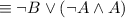 by Distributive law.
by Distributive law.
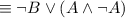 by the Commutative law.
by the Commutative law.
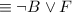 by the Negation law.
by the Negation law.
Therefore the statement
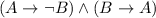 is a contingency.
is a contingency.
b) To classify the statement
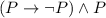 , you need to use the logic laws as follows:
, you need to use the logic laws as follows:
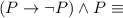
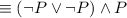 by the logical equivalence involving conditional statement.
by the logical equivalence involving conditional statement.
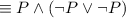 by the Commutative law.
by the Commutative law.
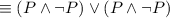 by Distributive law.
by Distributive law.
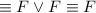 by the Negation law.
by the Negation law.
Therefore the statement
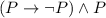 is a contradiction.
is a contradiction.