Question

To the nearest tenth, what is the perimeter of the triangle with vertices at (−2, 3), (3, 6), and (2, −2)?

Answer 1

The perimeter of triangle = 20.3

Explanation:

We need to find perimeter of the triangle with vertices at (−2, 3), (3, 6), and (2, −2)

The formula used to find perimeter is:
`Perimeter=Sum\:of\:length\:of\:all\:sides`

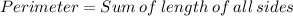
First we need to find length of each side using distance formula:

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

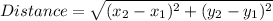
Find distance between (−2, 3), (3, 6)

We have:
`x_1=-2,y_1=3, x_2=3,y_2=6`

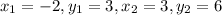
Putting values and finding distance

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)\\Distance=√((3-(-2))^2+(6-3)^2)\\Distance=√((3+2)^2+(6-3)^2)\\Distance=√((5)^2+(3)^2)\\Distance=√(25+9)\\Distance=√(34)\\Distance = 5.83`

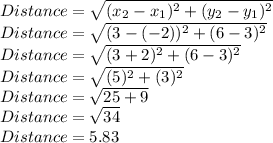
So, The distance between (−2, 3), (3, 6) is 5.83

Find distance between (3, 6),(2,-2)

We have:
`x_1=3,y_1=6, x_2=2,y_2=-2`

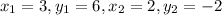
Putting values and finding distance

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)\\Distance=√((2-3)^2+(-2-6)^2)\\Distance=√((1)^2+(-8)^2)\\Distance=√(1+64)\\Distance=√(65)\\Distance=8.06`

So, The distance between (3, 6),(2,-2) is 8.06

Find distance between (-2,3),(2,-2)

We have:
`x_1=-2,y_1=3, x_2=2,y_2=-2`

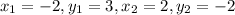
Putting values and finding distance

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)\\Distance=√((2-(-2))^2+(-2-3)^2)\\Distance=√((2+2)^2+(-2-3)^2)\\Distance=√((4)^2+(5)^2)\\Distance=√(16+25)\\Distance=√(41) \\Distance=6.40`

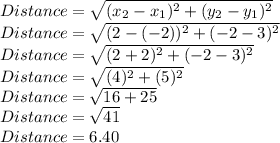
So, The distance between (-2, 3),(2,-2) is 6.40

So, The length of side 1 = 5.83

The length of side 2 = 8.06

The length of side 3 = 6.40

The perimeter of triangle will be:

`Perimeter=Sum\:of\:length\:of\:all\:sides\\Perimeter=5.83+8.06+6.40\\Perimeter=20.29\approx 20.3`

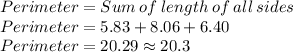
So, The perimeter of triangle = 20.3