Question

At a unit price of $700, the quantity demanded of a certain commodity is 90 pounds. If the unit price increases to $900, the quantity demanded decreases by 50 pounds. Find the demand equation (assuming it is linear) where p is the unit price and x is the quantity demanded for this commodity in pounds.

p =

At what price are no consumers willing to buy this commodity? $ _________

According to the above model, how many pounds of this commodity would consumers take if it was free? __________ pounds

Answer 1

Answer and explanation:

Given : At a unit price of $700, the quantity demanded of a certain commodity is 90 pounds. If the unit price increases to $900, the quantity demanded decreases by 50 pounds.

To find : 1) The demand equation ?

2) At what price are no consumers willing to buy this commodity?

3) According to the above model, how many pounds of this commodity would consumers take if it was free?

Solution :

Let 'p' is the unit price and 'x' is the quantity demanded for this commodity in pounds.

At a unit price of $700, the quantity demanded of a certain commodity is 90 pounds.

i.e.
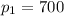`p_1=700` and
`x_1=90`

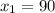
If the unit price increases to $900, the quantity demanded decreases by 50 pounds.

i.e.
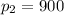`p_2=900` and
`x_2=90-50=40`

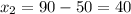
The relation between the price and demand is given by,

`(x-x_1)/(p-p_1)=(x_2-x_1)/(p_2-p_1)`

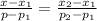
Substitute the values,

`(x-90)/(p-700)=(40-90)/(900-700)`

`(x-90)/(p-700)=(-50)/(200)`

`(x-90)/(p-700)=(-1)/(4)`

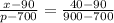
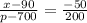
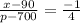
Cross multiply,

`4(x-90)=-1(p-700)`

`4x-360=-p+700`

`p=700+360-4x`

`p=1060-4x`

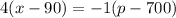
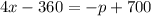
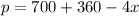
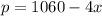
1) The demand equation is
`p=1060-4x`

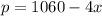
2) No consumer will buy commodity i.e. x=0

Substitute in the demand function,

`p=1060-4(0)`

`p=1060`

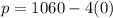
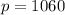
So, $1060 is the price where no consumers willing to buy this commodity.

3) If it is free means price became zero.

Substitute p=0 in the demand function,

`0=1060-4x`

`4x=1060`

`x=(1060)/(4)`

`x=265`

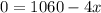
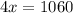
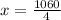
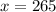
So, 265 pounds of this commodity would consumers take if it was free.