Question

A committee of 2 people is to be chosen from 5 women and 5 men. What is the probability at least one man was chosen given at least one woman was chosen?

Answer 1

5/9

Explanation:

At the beginning, there are 5 + 5 = 10 people to choose from. After one woman is chosen, that number goes down to 10 - 1 = 9 people. 5 men are still left to choose from, so there is a 5/9 chance at least one man will be selected as the other committee member.

Answer 2

5/7

Explanation:

Number of women = 5

Number of men = 5

2 people is to be chosen to form a committee.

Let as assume

A : At least one man was chosen

B : At least one woman was chosen

A ∩ B : Exactly one man and one woman was chosen

P(B) = Exactly one woman was chosen + Two women was chosen

`P(B)=(^5C_1* ^5C_1+^5C_0* ^5C_2)/(^(10)C_2)\Rightarrow (5* 5+1* 10)/(45)=(35)/(45)=(7)/(9)`

`P(A\cap B)=(^5C_1* ^5C_1)/(^(10)C_2)\Rightarrow (5* 5)/(45)=(25)/(45)=(5)/(9)`

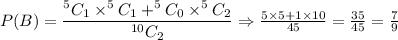
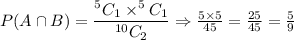
We need to find the probability at least one man was chosen given at least one woman was chosen.

`P((A)/(B))=(P(A\cap B))/(P(B))`

`P((A)/(B))=((5)/(9))/((7)/(9))`

`P((A)/(B))=(5)/(7)`

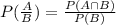
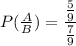
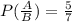
Therefore, the required probability is 5/7.