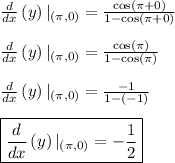Question

Given that y = sin(x+y),find the derivative when (x,y)=(π,0)​

Answer 1

Shown in the explanation

Explanation:

Recall that an implicit function is a relation given by the form:

`{\displaystyle R(x_(1),\ldots, x_(n))=0}`

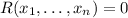
Where
`R` is a function of two or more variables. In this case, that function is:

`y = sin(x+y)`

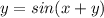
and is implicit because we can define it as:

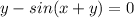`y-sin(x+y)=0` having two variables.

So, let's take the derivative:

`(d)/(dx)\left(y\right)=(d)/(dx)\left(\sin \left(x+y\right)\right) \\ \\`

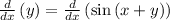
Applying chain rule:

`(d)/(dx)\left(\sin \left(x+y\right)\right)=\cos \left(x+y\right)\left(1+(d)/(dx)\left(y\right)\right)`

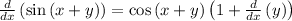
But:

`(d)/(dx)\left(y\right)=y'`

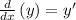
Therefore:

`y'=\cos \left(x+y\right)\left(1+y'\right)`

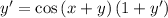
Isolating
`y'`:

`(d)/(dx)\left(y\right)=y'=(\cos \left(x+y\right))/(1-\cos \left(x+y\right))`

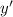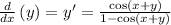
When
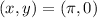`(x,y)=(\pi,0)`:

`(d)/(dx)\left(y\right)|_((\pi,0))=(\cos \left(\pi+0\right))/(1-\cos \left(\pi+0\right)) \\ \\ (d)/(dx)\left(y\right)|_((\pi,0))=(\cos \left(\pi\right))/(1-\cos \left(\pi\right)) \\ \\ (d)/(dx)\left(y\right)|_((\pi,0))=(-1)/(1-(-1)) \\ \\ \boxed(d)/(dx)\left(y\right)`