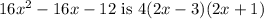Answer:
The factored form of
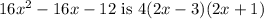
Solution:
From question, given that
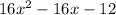
To factorize the given expression, follow the below steps:
 ---- eqn 1
---- eqn 1
Taking 4 as a common term in equation 1, we get
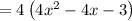
“4x” can be rewritten as –6x+2x. Now the above equation becomes,

By taking 2x as common from
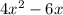 , the above equation becomes,
, the above equation becomes,
![=4[2x(2 x-3)+1(2 x-3)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/s4f0jyz36yj1egm7vwd0pr5u8ih8974dup.png)
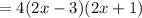
Hence the factor of