Answer:
Yes.
Explanation:
(Assume x is not 1.)
 is always divisible for integers greater than 1.
is always divisible for integers greater than 1.
Let's use synthetic division:
1 | 1x^n + 0x^(n-1) +0x^(n-2) + ....+0x^3+0x^2+0x -1
| 1 1 1 1 1 1
---------------------------------------------------------------------------------
1 1 1 1 1 1 0
We see the remainder is 0 which means that
 divides
divides
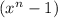 .
.
The quotient is
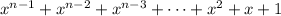 .
.