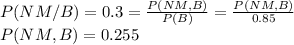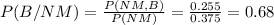Question

Alex’s motorcycle didn’t start this morning. He was not sure if it was because of the battery or a damaged starter. If he replaces the battery, the engine will run with probability 0.7. If he replaces the starter, it will run with probability 0.2. He can try one of these in an hour. I was 85% certain that he would replace the battery. If the engine doesn’t run in an hour, what is the probability that Alex replaced the battery (write it up to second decimal place)?

Answer 1

The probability is 0.68

Explanation:

We are going to use conditional probability to solve this problem.

We define the following events :

A : '' Alex replaced the starter''

B : ''Alex replaced the battery''

M : ''The engine works''

NM : ''The engine doesn't work''

Given two events A and B, we define the conditional probability:

`P(A/B) =(P(A,B))/(P(B)) \\P(B)> 0`

`P(B/A)=(P(B,A))/(P(A)) \\P(A)> 0`

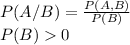
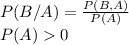
Where P(A,B) = P(B,A) = P(A∩B) = P(B∩A)

In our problem :

`P(M/B)=0.7\\P(M/A)=0.2\\P(B)=0.85\\`

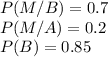
Alex replaced the battery or either the starter ⇒

`P(A)=1-P(B)=1-0.85=0.15\\P(A)=0.15`

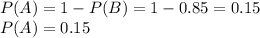
We need to find
`P(B/NM)=(P(B,NM))/(P(NM))`

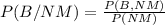
We write :

`P(M/B)=(P(M,B))/(P(B)) \\0.7=(P(M,B))/(0.85)\\ P(M,B)=0.595`

`P(M/A)=(P(M,A))/(P(A)) \\0.2=(P(M,A))/(0.15) \\P(M,A)=0.03`

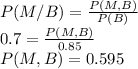
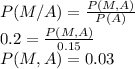
P(M) = [P(M∩B) ∪ P(M∩A)]

P(M) = P(M∩B) + P(M∩A) - P[(M∩B)∩(M∩A)]

But P[(M∩B)∩(M∩A)] = 0 because he replaced the battery or either the starter

P(M) = P(M∩B) + P(M∩A)

P(M)=0.595+0.03

P(M)=0.625

P(NM)= 1-P(M)=1-0.625=0.375

P(NM)= 0.375

P(NM/B) = 1-P(M/B)=1-0.7=0.3

P(NM/B) = 0.3

`P(NM/B)=0.3=(P(NM,B))/(P(B))=(P(NM,B))/(0.85) \\P(NM,B)=0.255`

`P(B/NM)=(P(NM,B))/(P(NM)) =(0.255)/(0.375) =0.68`