Question

Consider functions fand g.
f(x) = -13
g(x) = |1/8x-1|

Answer 1

We conclude that

(g o f) (4) = 9

Hence, option C is correct.

Explanation:

Given

f(x) = -x³

g(x) = |1/8x - 1|

To determine

(g o f) (4) = ?

Using the formula

(g o f) (4) = g[(f(4)]

first we need to determine f(4)

so substituting x = 4 into f(x) = -x³

f(x) = -x³

f(4) = -(4)³ = -64

so

(g o f) (4) = g[(f(4)] = g(-64)

so substitute x = -64 in g(x) = |1/8x - 1|

`g\left(x\right)=\left|(1)/(8)x-1\right|`

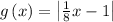
substitute x = -64

`g\left(-64\right)=\left|(1)/(8)\left(-64\right)-1\right|`

`=\left|-(1)/(8)\cdot \:64-1\right|`

`=\left|-8-1\right|`

`=\left|-9\right|`

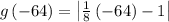
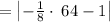
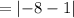
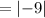
Apply absolute rule: |-a| = a

`=9`

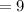
Therefore, we conclude that

(g o f) (4) = 9

Hence, option C is correct.