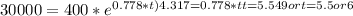Answer:
A)
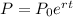
B)
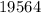
C)
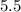 or
or
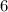 hours
hours
Step-by-step explanation:
A) The formula that can be used for bacteria after "t" hours is
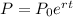
Where ,
 represents the population after "t" hours
represents the population after "t" hours
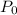 represents the initial population.
represents the initial population.
 represents the rate of growth of population
represents the rate of growth of population
 represents the time taken by the population to grow
represents the time taken by the population to grow
B) Here let us first find the rate of population growth.
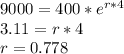
Thus, the population of bacteria after 5 hours
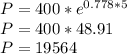
C)