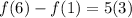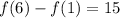Question

Please Explain

Given the formula for an arithmetic sequence f(6) = f(5) + 3 written using a recursive formula, write the sequence using an arithmetic formula.


f(6) = f(1) + 3

f(6) = f(1) + 12

f(6) = f(1) + 15

f(6) = f(1) + 18

Answer 1

f(6)=f(1)+15

Explanation:

Ok if f(6)-f(5)=3, then f(n)-f(n-1)=3 for any integer n greater than or equal to 2.

f(6)-f(1)

=(f(6)-f(5))+(f(5)-f(4))+(f(4)-f(3))+(f(3)-f(2))+(f(2)-f(1))

=(3) + (3) +(3) +(3) +(3)

=5(3)

=15

So the answer is the third one:

f(6)=f(1)+15

Arithmetic sequences are linear.

So no matter the points we choose, we should get the same slope.

`(f(6)-f(5))/(6-5)=(f(6)-f(1))/(6-1)=3`

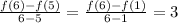
Both slopes are 3 since we were given term-previous term is 3.

`(f(6)-f(1))/(6-1)=3`

`(f(6)-f(1))/(5)=3`

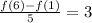
Multiply both sides by 5:

`f(6)-f(1)=5(3)`

`f(6)-f(1)=15`

`f(6)=f(1)+15`