Question

An investor can design a risky portfolio based on two stocks, A and B. Stock A has an expected return of 18% and a standard deviation of return of 20%. Stock B has an expected return of 14% and a standard deviation of return of 5%. The correlation coefficient between the returns of A and B is .50. The risk-free rate of return is 10%. The proportion of the optimal risky portfolio that should be invested in stock A is _________.

Answer 1

14%

Step-by-step explanation:

Let b = standard deviation of B

a = standard deviation of portfolio A

r = the correlation coefficient of both portfolios

We shall then proceed by calculating the weights for the optimal risky portfolios as:

W1 =
`(b^2-r *a * b)/(a^2 +b^2 -2r *a * b) \\\\= (0.05^2 -0.5 *0.2 *0.05)/(0.20^2 +0.05^2-2 *0.5*0.2*0.05) \\\\=`

=
`(0.0025-0.005)/(0.04 + 0.0025-0.01) =(-0.0025)/(0.0325) = -0.07692`

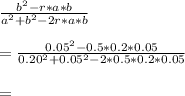
W2 = 1- W1 = 1- (-0.07692)

= 1 + 0.07692 = 1.07692

We shall then calculate the expected return for the optimal risky portfolio as

E(r) = W2R2 + W1R1

= (1.07692*0.14) + (-0.07692 *0.18)

=0.15076 -0.01384

= 0.1369

= 0.1369* 100 = 13.69%

= 14%