Question

Find the derivative of the function using the definition of derivative. g(t) = 9 t g'(t) = State the domain of the function. (Enter your answer using interval notation.) State the domain of its derivative. (Enter your answer using interval notation.)

Answer 1

domain [ g(t) ] = (-∞,∞)

g'(t)=9

domain [ g'(t) ] =(-∞,∞)

Explanation:

We start by finding the domain of the function g(t)

The domain of a function is the set of all inputs over which the function has defined outputs.

In g(t) = 9t ; g(t) is define for all real numbers

domain [ g(t) ] = (-∞,∞)

For the derivative of the function we use the definition of derivative :

Given f(x)→
`f'(x) = \lim_(h \to \00) (f(x+h)-f(x))/(h)`

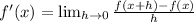
In our exercise :

`g'(t)= \lim_(h \to \00) (g(t+h)-g(t))/(h)`

`\lim_(h \to \00) (9(t+h)-9t)/(h) =\\ \lim_(h \to \00) (9t+9h-9t)/(h) =\\\lim_(h \to \00) (9h)/(h)\\\lim_(h \to \00) 9=9`

`g'(t)=9`

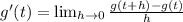
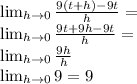
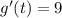
domain [ g'(t) ] =(-∞,∞)