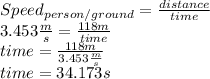Answer:
It takes 34.173 s
Step-by-step explanation:
This is a relative movement exercise.
We are going to use that :
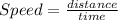
And the relative movement velocity equation :
Given a particle P, and two reference systems A and B in which we know the velocity from system B relative to A and the velocity of P relative to B :
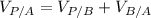
Don't forget that this is a vectorial equation.In our exercise the person velocity and the speed ramp velocity have the same direction so we turn the vectorial equation into a scalar equation.
We can cover 118 m in 76 s ⇒
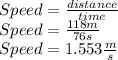
This will be our speed relative to the speed ramp
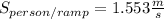
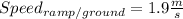
We use the equation (in terms of speed) :
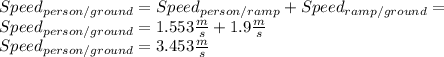
Then →