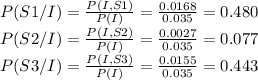Question

Three data entry specialists enter requisitions into a computer. Specialist 1 processes 42 percent of the requisitions, specialist 2 processes 27 percent, and specialist 3 processes 31 percent. The proportions of incorrectly entered requisitions by data entry specialists 1, 2, and 3 are 0.04, 0.01, and 0.05, respectively. Suppose that a random requisition is found to have been incorrectly entered. What is the probability that it was processed by data entry specialist 1? By data entry specialist 2? By data entry specialist 3? (Round your answers to 3 decimal places.)

Answer 1

The probabilities are 0.480;0.077 and 0.443 respectively

Explanation:

This is a conditional probability exercise.

Let's define conditional probability :

Given two events A and B :

`P(A/B)=(P(A,B))/(P(B)) \\P(B) > 0`

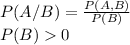
P(A,B) = P(A∩B) = P(B∩A) = P(B,A) : Is the probability that event A and event B occur at the same time.

We define the following events :

S1 : ''Specialist 1 processes requisitions''

S2 : ''Specialist 2 processes requisitions''

S3 : ''Specialist 3 preocesses requisitions''

I : ''Incorrect entered requisitions''

In our exercise :

`P(S1)=0.42\\P(S2)=0.27\\P(S3)=0.31\\P(I/S1)=0.04\\P(I/S2)=0.01\\P(I/S3)=0.05`

We are ask to find

`P(S1/I) ;P(S2/I);P(S3/I)`

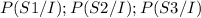
We write the conditional equations :

`P(I/S1)=(P(I,S1))/(P(S1)) \\0.04=(P(I,S1))/(0.42) \\P(I,S1)=0.0168`

`P(I/S2)=(P(I,S2))/(P(S2)) \\0.01=(P(I,S2))/(0.27) \\P(I,S2)=0.0027`

`P(I/S3)=(P(I,S3))/(P(S3)) \\0.05=(P(I,S3))/(0.31) \\P(I,S3)=0.0155`

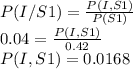
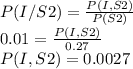
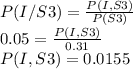
We also define

P(A∪B) = P(A) + P(B) - P(A∩B)

P(I) = P [(I,S1)∪(I,S2)∪(I,S3)]

`P(I) =P(I,S1) +P(I,S2)+P(I,S3)\\P(I)=0.0168+0.0027+0.0155\\P(I)=0.035`

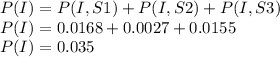
There is no intersection between (I,S1);(I,S2) and (I,S3) because they are mutually exclusive events.

`P(S1/I)=(P(I,S1))/(P(I)) =(0.0168)/(0.035) =0.480\\P(S2/I)=(P(I,S2))/(P(I)) =(0.0027)/(0.035) =0.077\\P(S3/I)=(P(I,S3))/(P(I)) =(0.0155)/(0.035) =0.443`