Question

Company A is considering building a new warehouse, which has 30% more square footage than the old warehouse. The old warehouse was constructed 9 years ago, with a cost of $20000. During the past 9 years, the cost of constucting a warehouse have risen by an average of 5% per year. If the cost-capacity factor, based on square footage, is 0.8, what would be the estimated cost of the new warehouse? Please round your answer to the nearest integer.

Answer 1

The cost of the new warehouse will be $38274

Step-by-step explanation:

For this calculation we can use the cost-capacity equation:

`C_(2) =C_(1) ((Q_(2) )/(Q_(1)))^(x)`

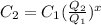
Where:

C2: Cost of new warehouse with known capacity Q2

C1: Cost of old warehouse with known capacity Q1

Q2: Capacity of new warehouse

Q1: Capacity of old warehouse

x: Cost-Capacity Factor

Let's consider Q1 as "Q", so Q2 will be "1.3Q", because the new warehouse will have a 30% more of capacity than the old one. x is equal to 0.8. Now, let's calculate C1 because the $20000 cost was nine years ago, so we have to calculate the present cost, which will be, C1.

For that, we can use this expression;
`C_(1)=PC*i^(n)`

Where:

PC: Present Cost of the warehouse; $20000

i: increment; that is 5% per year

n= number of years; 9

Replacing the data on the equation, we obtain:

`C_(1)=20000*1.05^(9) = $31027`

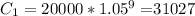
Now, we replace C1 on the first equation:

`C_(2) = 31027((1.3Q)/(Q))^(0.8)`

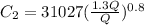
We can eliminate the "x" variable and make the operation.

C2 = $38274, we approximate to the next integer because we are talking about costs