Answer:
F1=177.88 Newtons
Step-by-step explanation:
Let's start with the Bernoulli's equation:
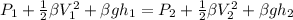
Where:
P is pressure, V is Velocity, g is gravity, h is height and β is density (for water β=1000 kg/m3); at the points 1 and 2 respectively.
From the Bernoulli's equation and assuming that h is constant and P2 is zero (from the data), we have:
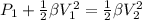
As we know, P1 must be equal to
 , so, replacing P1 in the equation, we have:
, so, replacing P1 in the equation, we have:
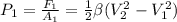
And
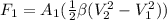
Now, let's find the velocity to replace the values on the expression:
We can express the flow in function of velocity and area as
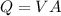 , where Q is flow, V is velocity and A is area. As the same, we can write this:
, where Q is flow, V is velocity and A is area. As the same, we can write this:
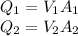 . In the last two equations, let's clear Velocities.
. In the last two equations, let's clear Velocities.
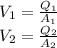
and replacing V1 and V2 on the last equation resulting from Bernoulli's (the one that has the force on it):
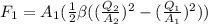
First, we have to consider that from a mass balance, the flow is the same, so Q1=Q2, what changes, is the velocity. Knowing this, let's write the areas, diameters, density and flow on International Units System (S.I.), because the exercise is asking us the answer in Newtons.
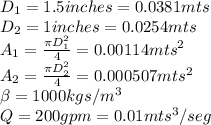
Replacing the respective values in this last expression, we obtain:
F1 = 177.88 N