Question

An infinite sheet of charge, oriented perpendicular to the x-axis, passes through x = 0. It has a surface charge density σ1 = -2.7 μC/m2. A thick, infinite conducting slab, also oriented perpendicular to the x-axis occupiees the region between a = 2.8 cm and b = 4.8 cm. The conducting slab has a net charge per unit area of σ2 = 88 μC/m2. What is Ex(P), the value of the x-component of the electric field at point P, located a distance 6.8 cm from the infinite sheet of charge?

Answer 1

The total electric field will be 5*10^5 N/C

Answer 2

`E_(total)=4.82*10^6N/C`

vector with direction equal to the axis X.

Step-by-step explanation:

We use the Gauss Law and the superposition law in order to solve this problem.

Superposition Law: the Total Electric field is the sum of the electric field of the first infinite sheet and the Electric field of the second infinite sheet:

`E_(total)=E_1+E_2`

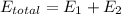
Thanks Gauss Law we know that the electric field of a infinite sheet with density of charge σ is:

`E=\sigma/(2\epsilon_o)`

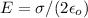
Then:

`E_(total)=(\sigma_1+\sigma_2)/(2\epsilon_o)=(-2.7*10^(-6)+88*10^(-6))/(2*8.85*10^(-12))=4.82*10^6N/C`

This electric field has a direction in the axis perpendicular to the sheets, that means it has the same direction as the axis X.