Question

A steel ball is dropped from a building's roof and passes a window, taking 0.115 s to fall from the top to the bottom of the window, a distance of 1.30 m. It then falls to a sidewalk and bounces back past the window, moving from bottom to top in 0.115 s. Assume that the upward flight is an exact reverse of the fall. The time spent below the bottom of the window is 2.04 s. How tall is the building?

Answer 1

The building is 26.85m tall.

Step-by-step explanation:

In order to solve this problem, we must start by drawing a diagram of the situation. (See attached picture).

We split the height of the building into three parts:
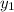`y_(1)`, the height of the window and
`y_2`

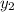
In order to find each of those, we need to start by finding the velocities of the ball in points A and B. We will analyze the trajectory of the ball when bouncing back to the top of the building. Let's start by finding the velocity of the ball in A:

We can use the following formula to determine the velocity of the ball in part A:

`\Delta y=V_(A)t+(1)/(2)at^(2)`

which can be solved for
`V_(A)`

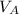
so we get:

`V_(A)=(\Delta y-(1)/(2)at^(2))/(t)`

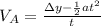
and now we can substitute (remember the acceleration of gravity goes downward so we will consider it to be negative).

`V_(A)=((1.30m)-(1)/(2)(-9.8m/s^(2))(0.115s)^(2))/(0.115s)`

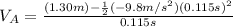
which yields:

`V_(A)=11.87m/s`

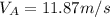
once we got the velocity at point A, we can now find the velocity at point B. We can do so by using the following formula:

`a=(V_(A)-V_(B))/(t)`

which can be solved for
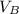`V_(B)` which yields:

`V_(B)=V_(A)-at`

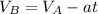
so we can substitute values now:

`V_(B)=11.87m/s-(-9.8)(0.115s)`

Which yields:

`V_(B)=13m/s`

Now that we have the velocities at A and B, we can use them to find the values of
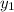`y_(1)` and
`y_(2)`

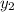
Let's start with
`y_(1)`

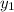
We can use the following formula to find it:

`y_(1)=(V_(f)^(2)-V_(A)^(2))/(2a)`

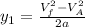
we know the final velocity of the rebound will be zero, so we can simplify our formula:

`y_(1)=(-V_(A)^(2))/(2a)`

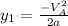
so we can substitute now:

`y_(1)=(-(11.87m/s)^(2))/(2(-9.8m/s^(2)))`

which solves to:

`y_(1)=7.19m`

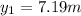
Now we can proceed and find the value of
`y_(2)`

the value of
`y_(2)` can be found by using the following formula:

`y_(2)=V_(B)t-(1)/(2)at^(2)`

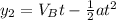
in this case our t will be half of the tie spent below the bottom of the window, so:

`t=(2.04s)/(2)=1.02s`

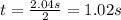
so now we can substitute all the values in the given formula:

`y_(2)=(13m/s)(1.02s)-(1)/(2)(-9.8m/s^(2))(1.02s)^(2)`

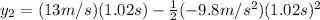
which yields:

`y_(2)=18.36m`

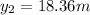
so now that we have all the values we need, we can go ahead and calculate the height of the building:

`h=y_(1)+window+y_(2)`

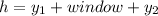
when substituting we get:

`h=7.19m+1.3m+18.36m`

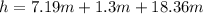
So the answer is:

h=26.85m

The building is 26.85m tall.